Como obtener la formula general de solución para las ecuaciones de segundo grado con una incógnita 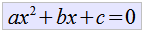 .
.
18-09-2008
Tenemos una ecuación de segundo grado con una incógnita cuya forma es ![]() . Sabemos también que
. Sabemos también que ![]() lo cual es un trinomio cuadrado perfecto, entonces empezaremos por completar el trinomio cuadrado perfecto en la ecuación cuadrática para con ello factorizar y en su caso despejar la x.
lo cual es un trinomio cuadrado perfecto, entonces empezaremos por completar el trinomio cuadrado perfecto en la ecuación cuadrática para con ello factorizar y en su caso despejar la x.
| Iniciamos con la ecuación de segundo grado con una incógnita. | |
| Dividimos todo entre |
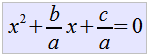 |
| Pasamos ahora el termino independiente al otro lado de la igualdad. Como se esta sumando, lo pasamos restando. | 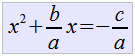 |
Tenemos ahora que completar el trinomio cuadrado prefecto 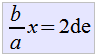 y nos queda que y nos queda que 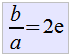 con lo que despejando con lo que despejando 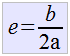 . Si queremos completar el trinomio cuadrado perfecto agregamos en ambos lados de nuestra igualdad . Si queremos completar el trinomio cuadrado perfecto agregamos en ambos lados de nuestra igualdad 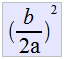 quedando como: quedando como: |
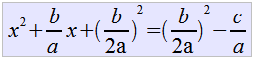 |
| Ya podemos factorizar el trinomio del elemento izquierdo de la igualdad y obtenemos el mínimo común denominador de la suma de fracciones del elemento derecho | 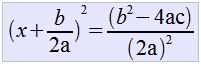 |
| Obtenemos la raíz cuadrada de ambos elementos de la igualdad. | 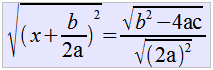 |
| En el primer elemento de la igualdad la raíz cuadrada con el cuadrado se anulan, pasando lo mismo con el dividendo del segundo elemento de la igualdad, quedando entonces | 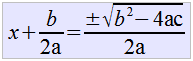 |
| Ahora solo falta despejar la x y debido a los dos posibles signos de nuestra última raíz cuadrada, obtendremos dos valores de x que validan nuestra ecuación, quedando entonces como la tan conocida formula general de solución de una ecuación de segundo grado con una incógnita. | 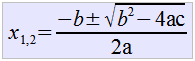 |
Recordemos que para aplicar esa formula ![]() debe ser diferente de cero, ya que en tal caso no estaríamos hablando de una ecuación de segundo grado si no de primer grado. En caso de que busquemos la solución dentro del conjunto de los números reales el contenido de la raíz debe ser no negativo, aunque si el contenido de la raíz fuera negativo, la solución esta en el conjunto de los números complejos.
debe ser diferente de cero, ya que en tal caso no estaríamos hablando de una ecuación de segundo grado si no de primer grado. En caso de que busquemos la solución dentro del conjunto de los números reales el contenido de la raíz debe ser no negativo, aunque si el contenido de la raíz fuera negativo, la solución esta en el conjunto de los números complejos.
Artículo relacionado:
Edgar F. Flores Muñoz
Comparte esta página Tweet
Tweet
escolar.mx
escolar.com.mx
Herramientas T.I. y noticias para Colegios, Profesores, Padres y Estudiantes.
Directorio de escuelas y colegios, desarrollo web para escuelas, ex�menes en l�nea, dise�o para centros educativos.
Lista de Artículos Disponibles
- Convocatoria UNAM concursos 2024
- COMIPEMS 2024 Concurso de ingreso al bachillerato
- Convocatoria UNAM concurso febrero 2020
- Convocatoria UNAM concurso junio 2020
- Convocatoria UNAM concurso noviembre 2020
- Convocatorias UNAM 2020
- COMIPEMS 2020 Concurso de ingreso al bachillerato
- Convocatoria UNAM concurso febrero 2019
- Convocatoria UNAM concurso junio 2019
- Convocatoria UNAM concurso noviembre 2019
- Convocatorias UNAM 2019
- COMIPEMS 2019 Concurso de ingreso al bachillerato
- Convocatoria UNAM concurso febrero 2018
- Convocatoria UNAM concurso junio 2018
- Convocatoria UNAM concurso noviembre 2018
- Convocatorias UNAM 2018
- Prepa en línea SEP - Convocatoria 2018 - 1
- COMIPEMS 2018 Concurso de ingreso al bachillerato
- Prepa en línea SEP - Convocatoria 2017 - 1
- Convocatoria UNAM concurso febrero 2017
- Convocatoria UNAM concurso junio 2017
- Convocatoria UNAM concurso noviembre 2017
- Convocatorias UNAM 2017
- COMIPEMS 2017 Concurso de ingreso al bachillerato
- Calendarios Escolares 2016 - 2017
- Convocatoria IPN 2016
- Prepa en línea SEP - Convocatoria 2016 - 1
- COMIPEMS 2016 Concurso de ingreso al bachillerato
- Convocatorias UNAM 2016
- Prepa en línea SEP - Convocatoria 2015 - 4
- Calendarios Escolares 2015 - 2016
- Prepa en línea SEP - Convocatoria 2015 - 3
- Convocatoria IPN 2015 - No Escolarizado
- Convocatoria UPN 2015
- Convocatoria UAM 2015
- Prepa en línea SEP - Convocatoria 2015 - 1
- Convocatorias UNAM 2015
- COMIPEMS 2015 Concurso de ingreso al bachillerato
- Convocatorias UNAM 2015
- COMIPEMS 2014 Concurso de ingreso al bachillerato
- Convocatorias UNAM 2014
- ENLACE 2014
- Calendarios Escolares 2013 2014
- Convocatorias IPN 2013
- 7mo Gran Remate de Libros en el Auditorio Nacional
- XXXIV Feria Internacional del Libro en el Palacio de Miner�a
- Convocatoria UAM 2013
- Concurso de ingreso al bachillerato 2013, COMIPEMS
- Convocatorias UNAM 2013
- ENLACE 2013
- Calendarios Escolares 2012-2013
- 6to Gran Remate de Libros en el Auditorio Nacional
- Convocatorias IPN 2012
- Convocatoria UAM 2012
- Convocatorias de ingreso a la UNAM 2012
- Concurso de ingreso al bachillerato 2012, COMIPEMS
- ESAD Licenciaturas abiertas y a distancia en la SEP 2011
- 3era Feria Educativa "Estudia sin fronteras" en la UNAM
- ENLACE 2012
- Calendario de escolar.com.mx
- Lista de �tiles 2011
- Calendarios Escolares 2011 2012
- Portal "Decide tu carrera"
- 5to Gran Remate de Libros en el Auditorio Nacional
- Convocatoria IPN 2011
- Google Art Project, proyecto de arte de Google.
- Prueba ENLACE 2011
- Convocatoria UAM 2011
- Concurso de ingreso al bachillerato 2011 (COMIPEMS)
- Convocatoria UNAM 2011
- Feria Internacional de Libro Guadalajara
- BigBlueButton. V�deo conferencia para ense�anza a distancia de c�digo abierto.
- Feria Internacional de Libro Infantil y Juvenil
- V�deo tutoriales de OpenOffice.org
- Open Office para niños, OO.org4Kids
- Calendarios Escolares 2010 - 2011
- 4to Remate de libros en el Auditorio Nacional
- Programa Conectar Igualdad, reparto de netbooks en Argentina
- Convocatoria Bellas Artes 2010
- ENLACE 2010
- Convocatoria IPN 2010
- Convocatoria UAM 2010
- Nuestro criterio de asignación de lugares a las escuelas por sus resultados en la prueba ENLACE
- Convocatoria UPN 2010
- Libera un libro
- Estar en Onda, Google Wave
- Escuelas de nivel medio superior de alta demanda, no pertenecientes a la UNAM ni al IPN
- Concurso de ingreso al bachillerato 2010 (COMIPEMS)
- Convocatorias UNAM 2010
- xiii Exposición "Al encuentro del mañana". Orientación vocacional 2009
- Las 10 escuelas con los mejores resultados en la prueba ENLACE 2009 por estado.
- Licenciaturas abiertas y a distancia en la SEP
- ENLACE 2009: Las 20 escuelas de educación media superior con los mejores resultados en la prueba
- Los niños imitan lo que ven. Campa�a DIF y Canal 11.
- Classmate PC en M�xico.
- Calendarios Escolares 2009 - 2010
- Sitios web de universidades mexicanas m�s visitados
- 3er Remate de Libros en el Distrito Federal
- Camstudio b�sico para hacer v�deo tutoriales
- Convocatoria de ingreso a la Universidad de Quintana Roo 2009, campus Riviera Maya
- UNAM gana premio Pr�ncipe de Asturias 2009
- Resultados de la prueba ENLACE
- Niños mexicanos e Internet, programa T.V. Sol�rzano en la red #85
- Twitter en la escuela.
Twitter, servicio de microblogging.� - �Por qu� todos deben aprender a programar?
- Convocatoria SUAyED UNAM 2009
- �Qu� carrera estudiar?
- D�a internacional del libro
- Convocatoria Bellas Artes 2009
- Biblioteca Digital Mundial de la UNESCO
- Por un uso responsable de las TIC en niños y adolecentes.
- Encarta se rinde ante Wikipedia
- Los buenos padres juegan videojuegos por Edgar F. Flores
- Convocatoria IPN 2009
- Los test de inteligencia, de lo global a lo regional por Ana Azuela
- Enlace 2009
- ¿Qui´enes son los niños talentosos y qu� sentido tiene desarrollarlos? por Ana Azuela
- Convocatoria UPN 2009
- Descarga Cultura UNAM
- Gu�a de videojuegos
- Contra el acoso por Internet.
- La SEP y Microsoft firman convenio para facilitar la compra de computadoras por parte de los alumnos de educación media.
- Aprendizaje cooperativo
- El ni�o creativo, por Ana Azuela
- Juguetes hechos de basura (Toys from trash)
- Scrabble de matem�tica
- Utilizando el talento de los niños para entrenar a los lideres del mañana por Ana Azuela.
- Convocatoria UAM 2009
- El ni�o construyendo al hombre por Ana Azuela
- Concurso de ingreso al bachillerato 2009
- CECyT del IPN (Vocacionales) de alta demanda
- El origen de un ni�o precoz por Ana Azuela
- CCH de la UNAM de alta demanda
- Preparatorias de la UNAM de alta demanda
� - �Tiene tu hijo un alto potencial? por Ana Azuela
- Programa Adopte un Talento (PAUTA)
� - Convocatorias UNAM 2009
� - El derecho a ser inteligente, por Ana Azuela
� - Generaciones Interactivas en Iberoam�rica.
Se present� en M�xico, Chile, Venezuela y Per� los resultados del estudio de las generaciones interactivas en iberoam�rica.
� - Firman la UNAM y TELMEX Convenio.
El convenio incluye la instalación de Aulas Telmex en todo el bachillerato de la UNAM.
� - OLPC, Dona 1 Obten 1
Esquema de comercialización con donativo para adquirir una XO
�� - "Yo Elijo mi PC"
Iniciativa del gobierno de Chile para acercar la tecnolog�a a los niños de escasos recursos.
� - Programa de Educación y Cultura Digital Telmex y Fundación Carlos Slim.
� - ANUIES presentar� ante la SEP propuesta de un Subsistema Nacional de Evaluación de la Educación Superior.
� - Al encuentro del mañana.
Exposición de Orientación Vocacional 2008.
� - Niñas y niños con talento.
Programa de est�mulos para menores destacados en las escuelas p�blicas del Distrito Federal.
� - Convocatoria UNAM Noviembre 2008 Sistema de Universidad Abierta
� - Kidsmart, iniciativa de IBM.
IBM busca apoyar la educación de los niños entre 3 y 6 a�os.
� - Congreso en Espa�a Internet en el Aula.
� - Como obtener la formula general de solución para las ecuaciones de segundo grado con una inc�gnita.
Demostración algebraica de como se genera la formula general de solución de las ecuaciones de segundo grado con una inc�gnita.
� - Instituto Nacional para la Educación de los Adultos (INEA).
Porque nunca es tarde para aprender.
� - Una laptop por ni�o. One laptop per child.
� - Inicio de Clases en M�xico, ciclo 2008 - 2009
� - Calendarios escolares 2008 - 2009
Aqu� encontraran la liga de algunos de los calendarios escolares 2008 - 2009 actualizados de las principales instituciones educativas de M�xico. - Resultados de la Prueba ENLACE 2008, se publicaran la �ltima semana de agosto.
Evaluación Nacional al Logro Acad�mico en Centros Escolares, ENLACE.
� - Bachillerato a Distancia para los habitantes de la Ciudad de M�xico.
La Secretaria de Educación del Distrito Federal ofrece la posibilidad de cursar el bachillerato a distancia sin costo para todos los habitantes de la Ciudad de M�xico. Esta es una posibilidad m�s en la oferta educativa de la Ciudad de M�xico.
� - Creando un Podcast con Audacity.
Demostración en video que nos muestra la forma b�sica de crear un podcast usando el programa de grabación y edición de audio Audacity. El art�culo contiene adem�s ligas hacia sitios donde se dan consejos para una mejor creación de podcast. - Dialectoteca del espa�ol.
Sitio de la Universidad de Iowa que nos permite conocer y escuchar diferentes dialectos del espa�ol. - Plataformas de elearning
Moodle, Claroline, Docebo y Dokeos. - Google Apps para Escuelas
�Deseas que tu organización cuente con herramientas de colaboración y comunicación sencillas y potentes sin tener que soportar las molestias habituales y el coste que suponen? - Navega Protegido en Internet usando Windows.
Sitio donde encontraremos recomendaciones tanto de software como de algunas practicas que pueden ayudarnos a mantenernos navegando en la red sin naufragar por sitios no deseables. - Foro : La universalización de la Educación Preescolar Mayo 2008.
La Secreteria de Educación de la Ciudad de M�xico organiza este foro en el centro cultural San Angel. - Convocatoria INBA 2008-2009.
Convocatoria para nivel profesional en las distintas ramas de las bellas artes en M�xico. - Generaciones I.
Encuestas sobre el uso de Internet de los niños y los jovenes de la Universidad de Navarra. - Nativos Digitales.
Niños y j�venes frente a la tecnolog�a - Convocatoria UNAM Junio 2008.
- Ranking de Universidades en el Mundo.
- Herakles, Sistema de Ex�menes en Línea.
Peque�o sistema hecho en Javascript para generar y calificar ex�menes basados en un banco de reactivos. - El nombre de dominio de tu escuela o colegio gr�tis .edu.mx
La imagen de tu institución siempre es importante, entonces �qu� esperas para registrar el nombre de dominio .edu.mx de tu escuela o colegio? - Concursos de Ingreso para nivel Bachillerato y Nivel Licenciatura.
Lista de p�ginas para el concurso de ingreso para las instituciones de nivel medio superior del valle de M�xico y para nivel licenciatura en la U.N.A.M. , I.P.N. y U.A.M. - Suite de Oficina gratuita para escuelas y colegios (de hecho, gratuita para todo mundo).
Adopta OpenOffice como parte del software para tu escuela, colegio o para t� mismo, ya se en casa o en el trabajo. - Solución a una ecuación de segundo grado con una inc�gnita usando Javascript.
La solución a una ecuación de segundo grado utilizando la formula general se implementa utilizando javascript, y se parte desde un algoritmo simple hasta uno m�s completo el cual incluso es capaz de dar la solución en el conjunto de los n�meros complejos.



